Higgs Boson The Oscillator

I-                  Introduction

In this post I would like to introduce you to the disinfection of the matrimonial baggers of the Lithuanian microscopic sediments. The essential point in this post is around Higgs boson mechanism;

means how, why, where, and when Higgs boson exercises it's influence on other subatomic particles?

What we already know is; that there are eleven nodes and eleven oscillators driven from the suggested supersymmetry theory which I explained through drawings and definitions published in earlier posts.

In particle physics the most important paradox is the annihilation of particles where quantum and momentum are conserved, the result of this paradox is the genesis of new exotic particles. 

Our subject here is the objection of the insurrection of Higgs boson mechanism. The main cause of the information below; which comes in two parts, a definition and a drawing is to understand the correlation between the properties inside the eleven oscillators.

Believe it or not!! Everything is built on the base of a sinusoidal wave exactly the same as the DNA; meanwhile the conjugation is the perfect key to discover the world of electronics.

Now the resolution is bright and clear to see Higgs boson as an oscillator. Please note that in each time new information is acquired; a definition and a drawing will be added to this post to explain our subject further more. And as long as there is no conclusion yet; this post will be in a state of continuity.

II-              Definitions and Drawings

1- A node: Is a point along a standing wave where the wave has minimal amplitude. For instance, in a vibrating guitar string, the ends of the string are nodes; by changing the position of the end’s node through frets, the guitarist changes the effective length of the vibrating string and thereby the note played. The opposite of a node is an anti-node; a point where the amplitude of the standing wave is a maximum this occurs midway between the nodes.

 2- Oscillator: Oscillation is the repetitive variation, typically in time, of some measure about a central value (often a point of equilibrium) or between two or more different states. Familiar examples include a swinging pendulum and AC power. The term vibration is sometimes used more narrowly to mean a mechanical oscillation but sometimes is used to be synonymous with "oscillation". Oscillations occur not only in physical systems but also in biological systems and in human society.

3- Acceleration:  The special theory of relativity describes the behaviour of objects travelling relatively to other objects at speeds approaching the speed of light in a vacuum. Newtonian mechanics is exactly revealed to be an approximation to reality, valid to great accuracy at lower speeds. As the relevant speeds increase toward the speed of light, acceleration no longer follows classical equations. As speeds approach the speed of light; the acceleration produced by a given force decreases and becomes asymptotically small as light speed is approached; an object with mass can approach this speed asymptotically but never reach it.

4- Energy and Matter, E = MC2: Energy can neither be created nor destroyed, and energy in all of it's forms has mass. Mass also can neither be created nor destroyed and in all of it's forms has energy. According to the theory of relativity; mass and energy as commonly understood are two names for the same thing, and neither one is changed nor transformed into the other. Rather, neither one exists without the other existing also, as a property of a system. Rather than mass being changed into energy the view of special relativity is; that rest mass has been changed to a more mobile form of mass, but remains mass. In the transformation process, neither the amount of mass nor the amount of energy changes, since both are properties which are connected to each other via a simple constant.

5- The Sine Wave or Sinusoid: Is a mathematical curve that describes a smooth repetitive oscillation. It is named after the function sine. It occurs often in pure and applied mathematics, as well as physics, engineering, signal processing and many other fields. The sine wave is important in physics because it retains it's wave shape when added to another sine wave of the same frequency and arbitrary phase and magnitude. It is the only periodic wave form that has this property. This property leads to it's importance in Fourier analysis and makes it acoustically unique.

6- Quarks Assumption: Is the state of quarks stability due Higgs boson oscillation.

7- Correlation Function: In statistical mechanics is a measure of the order in a system, as characterized by a mathematical correlation function, and describes how microscopic variables at different positions are correlated. In a spin system; it is the thermal average of the scalar product of the spins at two lattice points over all possible orderings.

8 - Free-Energy Relationship or Linear Gibbs Energy Relation: In physical organic chemistry, relates the logarithm of a reaction rate constant or equilibrium constant for one series of reactions with the logarithm of the rate or equilibrium constant for a related series of reactions. Establishing free-energy relationships helps in the understanding of the reaction mechanism for a chemical reaction and allows the prediction of reaction rates and equilibrium constants.

9- Higgs Boson Reconstructions: In addition “I know that the perception of Higgs boson contradictions is influenceable by accuracy; means that the conceptual is perfectionist. As human precision is incapable to detect these occurrences of Higgs boson reconstructions, in spite of all technologies used to understand it, it is still a mystery.” In condition “substrates are subsequent of Higgs boson mechanism; means that the conceptual is definitely right, because instead of limiting the conceptual, a serious investigation of what it has been presented in this blog would be a wise reasoning”.

10- Recreation of the Hypothetical Higgs Boson: We already know that Higgs boson is an insulator (Please check “Ink and Diamond post”), what is fundamental is that the assumption is equal to a sentinel in cryptology. Higgs boson insurrection on physical laws is plausible upon the conjugated systems, where molecules are joined through p-bonding; this explain the insulation of the universe and the existence of holes where electrons, protons and gamma rays are free to travel horizontally and vertically, nothing else is allowed to do so. On my experiment on Rugosa corals (Higgs boson) the production of diamond was possible due the joined gathering of carbon atoms through P-bonding; this represents a conjugated system in itself. The invocation of letter conjugation in Figure (F22a) is a perfect explanation to Higgs boson insurrection and insulation.

11- Higgs Boson Assumptions: Are the states where Higgs boson becomes stable, in the figure bellow we can see (6) forms of assumption representing Higgs boson stability.

12- Higgs Boson Manifesto: Unconditional substrates are the key to innovation; in addition “I think that the conception is a valuable thing, so the interactions of the connected subatomic particles are due to Higgs boson oscillation. The conception is decisive, metamorphic and soluble”.

13- Higgs Boson Decoding: Is a substantial catenation to the aberration of the insulin.

14- Higgs Boson Auto-Destruction:

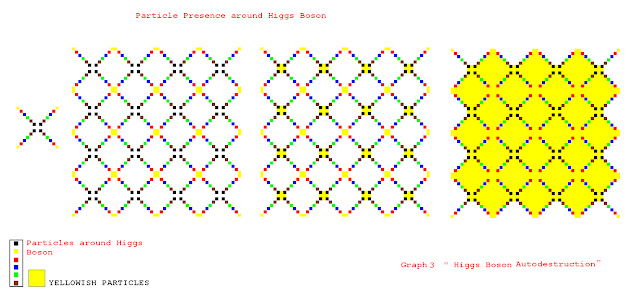
14- 1 Particle Connection around Higgs Boson: The availability of Higgs Boson is the perfect way to understand it’s destruction; by looking at the graph shown bellow we understand the composition and the manners of the cycle of the particles participating in the destruction of Higgs boson.

The different colours used are taking places to show the connection of these particles around Higgs boson. The list of the particles is indeterminate yet, and is indefinite. As I said my experiment is still live and each time a particle is generated; it’s addition will appear on future graphs. Remember in the super symmetry the particles are spread in latitude and altitude manner.

14-2 Particle Influence on Higgs Boson: Systematic has a grand role in defining the kind of particles which are around Higgs boson. Let’s suggesting that the blue particles are “Mamers”; their number grows from (12) to (48). Now we know that there are (48) different particles under different names and they have different characteristics. Not only that but they can develop to the infinite. In the first case “Bottom left” the commemoration is forbidden as it has a straight link to Higgs boson.

14-3 Particle Presence around Higgs Boson: Particle Presence is an indirect obstacle that permitting innovation of Higgs boson Cycle. The yellow particles shown on the Graph (3) have an indefinite number; their participation in Higgs boson Cycle is imminent, these are called “Yellowish Particles”.

14-4 Particle Physics Manipulation: Is a wonderful era of imagination of Particle Physics beyond humans' knowledge. Thus manufacturing could take a great advantage by opening their pockets in order to substitute the correlation between particle Physics and the industrial world.

14-5 Higgs Boson Arrows: The constitution of Higgs boson is unknown and flat; meanwhile the paparazzi are giants to human eye, the subject here is to suggest the idea of Higgs boson Arrows; they are simple particles with red colour, they are capable to transferee ammunition to the heart of Higgs boson, by this an electromagnetic field is created. I also found that “Reddish” is a suitable name to this kind of particles.

14-6 Higgs Boson Manifestation: Brownish Particles are supposed to be the first in the trinity due to their colour charge.

III     Conclusion

After all what it has been said is just a hypothesis in which the reader may find a work of art. This post comes to it’s end, in consequence by joining the matter at it’s end; accordingly frames are still under observation. The question is; do we require a more sophisticated technology? I suppose yes.

Understandable Matter (BECs Phase 6)

HYPOTHESIS

I would like to say my word to make the cleavage between the known and the unknown of dark matter. Through Bose Einstein Condensate system (BECs) Phase (6), I conclude that Dark matter is represented in (3) forms (Majorana fermions, Glueballs and Phosphorus).

In the photographs bellow we can see Majorana fermions and Glueballs generated within the system (BECs) as huge condensate matter.

Majorana fermions and Glue balls

Majorana fermions and Glue balls

Majorana fermions and Glue balls under the High Temperature Superconductor

Definition I

1- Dark matter, in astronomy and cosmology, dark matter is a type of matter hypothesized to account for a large part of the total mass in the universe. Dark matter cannot be seen directly with telescopes; evidently it neither emits nor absorbs light or other electromagnetic radiation at any significant level. Instead, its existence and properties are inferred from its gravitational effects on visible matter, radiation, and the large scale structure of the universe. Dark matter is estimated to constitute 84% of the matter in the universe and 23% of the mass-energy

According to consensus among cosmologists, dark matter is composed primarily of a new, not yet characterized, type of subatomic particle. The search for this particle, by a variety of means, is one of the major efforts in particle physics today.

Although the existence of dark matter is generally accepted by the mainstream scientific community, several alternative theories have been proposed to try to explain the anomalies for which dark matter is intended to account.

2- Dark Matter Detection

2-1 Direct Detection Experiments

Direct detection experiments typically operate in deep underground laboratories to reduce the background from cosmic rays. These include: the Soudan mine; the SNOLAB underground laboratory at Sudbury, Ontario (Canada); the Gran Sasso National Laboratory (Italy); the Canfranc Underground Laboratory (Spain); the Boulby Underground Laboratory(UK); and the Deep Underground Science and Engineering Laboratory, South Dakota (US).

The majority of present experiments use one of two detector technologies: cryogenic detectors, operating at temperatures below 100mK, detect the heat produced when a particle hits an atom in a crystal absorber such as germanium. Noble liquid detectors detect the flash of scintillation light produced by a particle collision in liquid xenon or argon. Cryogenic detector experiments include: CDMS, CRESST, EDELWEISS, and EURECA. Noble liquid experiments include ZEPLIN, XENON, DEAP, ArDM, WARP and LUX. Both of these detector techniques are capable of distinguishing background particles which scatter off electrons, from dark matter particles which scatter off nuclei. Other experiments include SIMPLE and PICASSO.

The DAMA/NaI, DAMA/LIBRA experiments have detected an annual modulation in the event rate, which they claim is due to dark matter particles. (As the Earth orbits the Sun, the velocity of the detector relative to the dark matter halo will vary by a small amount depending on the time of year). This claim is so far unconfirmed and difficult to reconcile with the negative results of other experiments assuming that the WIMP scenario is correct.

Directional detection of dark matter is a search strategy based on the motion of the Solar System around the galactic centre.

By using a low pressure TPC, it is possible to access information on recoiling tracks (3D reconstruction if possible) and to constrain the WIMP-nucleus kinematics. WIMPs coming from the direction in which the Sun is travelling (roughly in the direction of the Cygnus constellation) may then be separated from background noise, which should be isotropic. Directional dark matter experiments include DMTPC, DRIFT, Newage and MIMAC.

On 17 December 2009 CDMS researchers reported two possible WIMP candidate events. They estimate that the probability that these events are due to a known background (neutrons or misidentified beta or gamma events) is 23%, and conclude "this analysis cannot be interpreted as significant evidence for WIMP interactions, but we cannot reject either event as signal."

More recently, on 4 September 2011, researchers using the CRESST detectors presented evidence of 67 collisions occurring in detector crystals from sub-atomic particles, calculating there is a less than 1 in 10,000 chance that all were caused by known sources of interference or contamination. It is quite possible then that many of these collisions were caused by WIMPs, and/or other unknown particles.

2-2 Indirect Detection Experiments

Indirect detection experiments search for the products of WIMP annihilation. If WIMPs are Majorana particles (the particle and antiparticle are the same) then two WIMPs colliding could annihilate to produce gamma rays or particle-antiparticle pairs. This could produce a significant number of gamma rays, antiprotons or positrons in the galactic halo. The detection of such a signal is not conclusive evidence for dark matter, as the production of gamma rays from other sources is not fully understood.

The EGRET gamma ray telescope observed more gamma rays than expected from the Milky Way, but scientists concluded that this was most likely due to an error in estimates of the telescope's sensitivity. The Fermi Gamma-ray Space Telescope, launched June 11, 2008, is searching for gamma ray events from dark matter annihilation.

At higher energies, ground-based gamma-ray telescopes have set limits on the annihilation of dark matter in dwarf spheroidal galaxies and in clusters of galaxies.

The PAMELA experiment (launched 2006) has detected a larger number of positrons than expected. These extra positrons could be produced by dark matter annihilation, but may also come from pulsars. No excess of anti-protons has been observed.

A few of the WIMPs passing through the Sun or Earth may scatter off atoms and lose energy. This way a large population of WIMPs may accumulate at the centre of these bodies, increasing the chance that two will collide and annihilate. This could produce a distinctive signal in the form of high-energy neutrinos originating from the centre of the Sun or Earth. It is generally considered that the detection of such a signal would be the strongest indirect proof of WIMP dark matter. High-energy neutrino telescopes such as AMANDA, IceCube and ANTARES are searching for this signal.

WIMP annihilation from the Milky Way Galaxy as a whole may also be detected in the form of various annihilation products. The Galactic center is a particularly good place to look because the density of dark matter may be very high there.

Phosphorus is Dark Matter

Phosphorus, is a chemical element with symbol P and atomic number 15. A multivalent non-metal of the nitrogen group, phosphorus as a mineral is almost always present in its maximally oxidised state, as inorganic phosphate rocks. Elemental phosphorus exists in two major forms white phosphorus and red phosphorus but due to its high reactivity, phosphorus is never found as a free element on Earth.

Phosphorus is essential for most life. As phosphate, it is a component of DNA, RNA, ATP, and also the phospholipids that form all cell membranes. Demonstrating the link between phosphorus and life, elemental phosphorus was historically first isolated from human urine, and bone ash was an important early phosphate source. Phosphate minerals are fossils. Low phosphate levels are an important limit to growth in some aquatic systems. The chief commercial use of phosphorus compounds for production of fertilisers is due to the need to replace the phosphorus that plants remove from the soil.

Definition II

1- Majorana Fermion, also referred to as a majorana particle, or simply, a majorana, is a fermionn that is its own antiparticle. The term is sometimes used in opposition to Dirac fermion, which describes particles that differ from their antiparticles. It is common that boson (such as the photon) are their own antiparticle. It is also quite common that fermions can be their own antiparticle, such as the fermionic quasiparticles in spin-singlet superconductors (where the quasiparticles/Majorana-fermions carry spin-1/2) and in superconductors with spin-orbital coupling, such as iridium, (where the quasiparticles/Majorana-fermions do not carry well defined spins).

2- In particle physics, a fermion (a name coined by Paul Dirac from the surname of Enrico Fermi) is any particle characterized by Fermi–Dirac statistics and following the Pauli Exclusion Principle; fermions include all quarks and leptons, as well as any composite particle made of an odd number of these, such as all baryons and many atoms and nuclei. Fermions contrast with bosons which obey Bose–Einstein statistics.

A fermion can be an elementary particle, such as the electron; or it can be a composite particle, such as the proton. The spin-statistics theorem holds that, in any reasonable relativistic quantum field theory, particles with integer spin are bosons, while particles with half-integer spin are fermions.

In contrast to bosons, only one fermion can occupy a particular quantum state at any given time. If more than one fermion occupies the same physical space, at least one property of each fermion, such as its spin, must be different. Fermions are usually associated with matter, whereas bosons are generally force carrier particles; although in the current state of particle physics the distinction between the two concepts is unclear.

The Standard Model recognizes two types of elementary fermions: quarks and leptons. In all, the model distinguishes 24 different fermions: 6 quarks and 6 leptons, each with a corresponding anti-particle.

Composite fermions, such as protons and neutrons, are key building blocks of matter. Weakly interacting fermions can also display bosonic behavior under extreme conditions, such as in superconductivity.

Definition III

1-Glueball, In particle physics, a glueball is a hypothetical composite particle. It consists solely of gluon particles, without valence quarks. Such a state is possible because gluons carry color charge and experience the strong interaction. Glueballs are extremely difficult to identify in particle accelerators, because they mix with ordinary meson states.

Theoretical calculations show that glueballs should exist at energy ranges accessible with current collider technology. However, due to the aforementioned difficulty, they have (as of 2011) so far not been observed and identified with certainty.

2- Gluons, are elementary particles that act as the exchange particles (or gauge bosons) for the strong force between quarks, analogous to the exchange of photons in the electromagnetic force between two charged particles.

Since quarks make up the baryons and the mesons, and the strong interaction takes place between baryons and mesons, one could say that the color force is the source of the strong interaction, or that the strong interaction is like a residual color force that extends beyond the baryons, for example when protons and neutrons are bound together in a nucleus.

In technical terms, they are vector gauge bosons that mediate strong interactions of quarks in quantum chromodynamics (QCD). Unlike the electrically neutral photon of quantum electrodynamics (QED), gluons themselves carry color charge and therefore participate in the strong interaction in addition to mediating it, making QCD significantly harder to analyze than QED.

3- Experiment and Observation, Quarkss and gluons (colored) manifest themselves by fragmenting into more quarks and gluons, which in turn hadronize into normal (colorless) particles, correlated in jets. As shown in 1978 summer conferences the PLUTO experiments at the electron-positron collider DORIS (DESY) reported the first evidence that the hadronic decays of the very narrow resonance Y(9.46) could be interpreted as three-jet event topologies produced by three gluons. Later published analyses by the same experiment confirmed this interpretation and also the spin 1 nature of the gluon (see also the recollection and PLUTO experiments).

In summer 1979 at higher energies at the electron-positron  collider PETRA (DESY) again three-jet topologies were observed, now interpreted as qq gluon bremsstrahlung, now clearly visible, by TASSO, MARK-J and PLUTO experiments (later in 1980 also by JADE). The spin 1 of the gluon was confirmed in 1980 by TASSO and PLUTO experiments (see also the review). In 1991 a subsequent experiment at the LEP storage ring at CERN again confirmed this result.

The gluons play an important role in the elementary strong interactions between quarks and gluons, described by QCD and studied particularly at the electron-proton collider HERA at DESY. The number and momentum distribution of the gluons in the proton (gluon density) have been measured by two experiments, H1 and ZEUS,  in the years 1996 till today (2012). The gluon contribution to the proton spin has been studied by the HERMES experiment at HERA. The gluon density in the photon (when behaving hadronically) has also been measured.

Color confinement is verified by the failure of free quark searches (searches of fractional charges). Quarks are normally produced in pairs (quark + antiquark) to compensate the quantum color and flavor numbers; however at Fermilab single production of top quarks has been shown. No glueball has been demonstrated.

Deconfinement was claimed in 2000 at CERN SPS in heavy-ion collisions, and it implies a new state of matter: quark-gluon plasma, less interacting than in the nucleus, almost as in a liquid. It was found at the Relativistic Heavy Ion Collider (RHIC) at Brookhaven in the years 2004–2010 by four contemporaneous experiments. A quark-gluon plasma state has been confirmed at the CERN Large Hadron Collider (LHC) by the three experiments ALICE, ATLAS and CMS in 2010.

 Definitions are from Wikipedia

Beyond Your Knowledge (BECs Phase 4)

Beyond Your Knowledge is my new album which deserves to be watched and shared. Through the following photographs an idea about how a New High Temperature Superconductor Material and Majorana fermions look like.

The Bose Einstein Condensate system (BECs) is the target, it is a closed system constructed by a superconductor and super fluid material; within this last a beautiful shapes of matter floating made of Majorana fermions, while another one formed at the bottom in hyperbolic shape.

I welcome you to the link below to watch pictures created by myself

https://plus.google.com/photos/117229018594189940785/albums/6100362860459806977?authkey=CJTp8K7ezbC7uwE

BECs Surface "Electron Density"

The video below is showing Bose Einstein Condensate system (BECs) surface. A High Temperature Superconductor or substrates formed on the top of the system to close it; and these substrates are unique materials made of copper and oxygen called cuprates and combine with Titanium, Dysprosium, and Silicon. The light is reflected in an angle of (45) degrees which is spread in very tiny bits due to electron density.

I would like to make a short explanation to expose the whole experiment from the beginning (from day one). The idea is about the discovery of Higgs boson which is incarnated within the Rugosa corals. To create Bose Einstein Condensate system (BECs) (6) Rugosa corals are needed that means that the total (6) represents Higgs boson.

Higgs boson is a monopole that means that (2) parts (Rugosa corals) will work as south poles, another (2) will work as north poles and the two left will be the neutrals or mediators between the south poles and the north poles.

By adding seawater a magnetic field is created, at this stage the most important path is that the system should be isolated or closed and this happens by the ejection of the carbon atoms first, this is why we saw that Graphene and diamond where first to appear on the surface as first layers to be generated. After that the copper and the oxygen form compounds with light metals such as Titanium, Dysprosium and Silicon; they travel to the surface to form (3) compounds (TiCuO, DyCuO and SiCuO). The atoms within the system loose their electrons and become equal in mass; the electrons rush to the surface to make it very dense and participate in the reflection of light.

I do believe that the compounds (TiCuO, DyCuO and SiCuO) are the perfect materials to be used as superconductors in room temperature to innovate the 3D chip and transistor manufacturing as they have a very high electron density.

The pictures below are showing Bose Einstein Condensate system (BECs) surface during my experiment on Higgs Boson inside the system.

Unconditional Substrates are the Key to Innovation

This post comes with complementary information to the two earlier posts of “True Bose Einstein Condensed System Phase( 3)”.

Definitions:

1-In quantum mechanics, the uncertainty principle: is any of a variety of mathematical inequalities asserting a fundamental lower bound on the precision with which certain pairs of physical properties of a particle, such as position (x) and momentum p, can be simultaneously known. The more precisely the position of some particle is determined, the less precisely its momentum can be known, and vice versa. The original heuristic argument that such a limit should exist was given by Werner Heisenberg in 1927.

Mathematically, the uncertainty relation between position and momentum arises because the expressions of the wave function in the two corresponding bases are Fourier transforms of one another (i.e., position and momentum are conjugate variables). A similar tradeoff between the variances of Fourier conjugates arises wherever Fourier analysis is needed, for example in sound waves. A pure tone is a sharp spike at a single frequency. Its Fourier transform gives the shape of the sound wave in the time domain, which is a completely delocalized sine wave. In quantum mechanics, the two key points are that the position of the particle takes the form of a matter wave, and momentum is its Fourier conjugate, assured by the de Broglie relation.

2- The Fourier transform, named for Joseph Fourier, is a mathematical transform with many applications in physics and engineering. Very commonly, it expresses a mathematical function of time as a function of frequency, known as its frequency spectrum. The Fourier integral theorem details this relationship. For instance, the transform of a musical chord made up of pure notes (without overtones) expressed as amplitude as a function of time, is a mathematical representation of the amplitudes and phases of the individual notes that make it up. The function of time is often called the time domain representation, and the frequency spectrum the frequency domain representation. The inverse Fourier transform expresses a frequency domain function in the time domain. Each value of the function is usually expressed as a complex number (called complex amplitude) that can be interpreted as a magnitude and a phase component. The term "Fourier transform" refers to both the transform operation and to the complex-valued function it produces.

3- In mathematics, Fourier analysis is the study of the way general functions may be represented or approximated by sums of simpler trigonometric functions. Fourier analysis grew from the study of Fourier series, and is named after Joseph Fourier, who showed that representing a function as a sum of trigonometric functions greatly simplifies the study of heat propagation.

4- Harmonic analysis: is a branch of mathematics concerned with the representation of functions or signals as the superposition of basic waves, and the study of and generalization of the notions of Fourier series and Fourier transforms. In the past two centuries, it has become a vast subject with applications in areas as diverse as signal processing, quantum mechanics, and neuroscience.

5- In signal processing, time–frequency analysis comprises those techniques that study a signal in both the time and frequency domains simultaneously, using various time–frequency representations. Rather than viewing a 1-dimensional signal (a function, real or complex-valued, whose domain is the real line) and some transform (another function whose domain is the real line, obtained from the original via some transform), time–frequency analysis studies a two-dimensional signal – a function whose domain is the two-dimensional real plane, obtained from the signal via a time–frequency transform.

6- Time frequency transform: In signal processing terms, a function (of time) is a representation of a signal with perfect time resolution, but no frequency information, while the Fourier transform has perfect frequency resolution, but no time information. As alternatives to the Fourier transform, in time–frequency analysis, one uses time–frequency transforms to represent signals in a form that has some time information and some frequency information – by the uncertainty principal, there is a trade-off between these. These can be generalizations of the Fourier transform, such as the short-time Fourier transform, the Gabor transform or fractional Fourier transform, or can use different functions to represent signals, as in wavelet transforms and chirplet transforms, with the wavelet analog of the (continuous) Fourier transform being the continuous wavelet transform.

7- The sine wave or sinusoid is a mathematical function that describes a smooth repetitive oscillation. It occurs often in pure and applied mathematics, as well as physics, engineering, signal processing and many other fields. Its most basic form as a function of time (t) is:

where:

A, the amplitude, is the peak deviation of the function from its center position.

ω, the angular frequency, specifies how many oscillations occur in a unit time interval, in radian per second

φ, the phase, specifies where in its cycle the oscillation begins at (t = 0).

When the phase is non-zero, the entire waveform appears to be shifted in time by the amount φ/ω seconds. A negative value represents a delay, and a positive value represents an advance.

7-1 This wave pattern occurs often in nature, including ocean waves, sound waves, and light waves.

A cosine wave is said to be "sinusoidal", because it is also a sine wave with a phase-shift of (π/2). Because of this "head stars", it is often said that the cosine function leads the sine function or the sine lags the cosine.

7-2 In two or three spatial dimensions, the same equation describes a travelling plane wave if position (x) and wave number (k) are interpreted as vectors, and their product as a dot product. For more complex waves such as the height of a water wave in a pond after a stone has been dropped in, more complex equations are needed.

7-3 In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers (usually coordinate vectors) and returns a single number obtained by multiplying corresponding entries and then summing those products. The name "dot product" is derived from the centered dot "  " that is often used to designate this operation; the alternative name "scalar product" emphasizes the scalar (rather than vector) nature of the result.

When two Euclidean vectors are expressed in terms of coordinate vectors on an orthonormal basis, the inner product of the former is equal to the dot product of the latter. For more general vector space, while both the inner and the dot product can be defined in different contexts (for instance with complex numbers as scalars) their definitions in these contexts may not coincide.

In three dimensional space, the dot product contrasts with the cross product, which produces a vector as result. The dot product is directly related to the cosine of the angle between two vectors in Euclidean space of any number of dimensions.

8- Signal processing: is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, or measurements of time-varying or spatially-varying physical quantities. Signals of interest can include sound, images, and sensor data, for example biological data such as electrocardiograms, control system signals, telecommunication transmission signals, and many others.

9- The goals of signal processing can roughly be divided into the following categories.

9-1 Signal acquisition and reconstruction, which involves measuring a physical signal, storing it, and possibly later rebuilding the original signal or an approximation thereof. For digital systems, this typically includes sampling and quantization.

9-1-1 Data acquisition: is the process of sampling signals that measure real world physical conditions and converting the resulting samples into digital numeric values that can be manipulated by a computer. Data acquisition systems (abbreviated with the acronym DAS or DAQ) typically convert analog waveforms into digital values for processing. The components of data acquisition systems include:

a) Sensors that convert physical parameters to electrical signals.

b) Signal conditioning circuitry to convert sensor signals into a form that can be converted to digital values.

c) Analog-to-digital converters, which convert conditioned sensor signals to digital values.

9-2 Quality improvement, such as noise reduction, image enhancement, and echo cancellation.

9-3 Signal compression, including audio compression, image compression, and video compression.

9-4 Feature extraction, such as image understanding and speech recognition.

9- 5 In communication systems, signal processing may occur at OSI layer (1), the Physical Layer (modulation, equalisation, multiplexing, etc.) in the seven layer OSI model, as well as at OSI layer (6), the Presentation Layer (source coding, including analog-to-digital conversion and data compression).

10- The Open Systems Interconnection (OSI) model: is a product of the Open Systems Interconnection effort at the International Organization for Standardization. It is a prescription of characterising and standardising the functions of communication system in terms of abstraction layers. Similar communication functions are grouped into logical layers. A layer serves the layer above it and is served by the layer below it.

According to recommendation X.200, there are seven layers, labelled (1) to (7), with layer (1) at the bottom. Each layer is generically known as an (N) layer. An "N+1 entity" (at layer N+1) requests services from an "N entity" (at layer N).

10-1 The (OSI) seven layers:

OSI Model
Polymer.doc	Data unit	Layer	Function
Host layers	Data	7. Application	Network process to application
		6. Presentation	Data representation, encryption and decryption, convert machine dependent data to machine independent data
		5. Session	Interhost communication, managing sessions between applications
	Segments	4. Transport	End-to-end connections, reliability and flow control
Media layers	Packet/Datagram	3. Network	Path determination and logical addressing
	Frame	2. Data link	Physical addressing
	Bit	1. Physical	Media, signal and binary transmission

11- Line vector: A line vector is a vector, such as a force, that is constrained to lie along a given line.

12- A transistor: is a semiconductor device used to amplify and switch electronic signals and electrical power. It is composed of a semiconductor material with at least three terminals for connection to an external circuit. A voltage or current applied to one pair of the transistor's terminals changes the current flowing through another pair of terminals. Because the controlled (output) power can be higher than the controlling (input) power, a transistor can amplify a signal. Today, some transistors are packaged individually, but many more are found embedded in integrate circuit.

13-1 Semiconductor devices: are electronic components that exploit the electronic properties of semiconductor materials, principally silicon, germanium, and gallium arsenide, as well as organic semiconductor. Semiconductor devices have replaced thermionic devices (vacuum tubes) in most applications. They use electronic conduction in the solid state as opposed to the gaseous or thermionic emission in a high vacuum.

13-2 An electron hole is the conceptual and mathematical opposite of an electron, useful in the study of physics, chemistry, and electrical engineering. The concept describes the lack of an electron at a position where one could exist in an atom or atomic lattice. It is different from the positron, which is an actual particle of antimatter, whereas the hole is just a fiction, used for modelling convenience.

The electron hole was introduced into calculations for the following two situations:

If an electron is excited into a higher state it leaves a hole in its old state. This meaning is used in Auger electron spectroscopy (and other x-ray techniques), in computational chemistry, and to explain the low electron-electron scattering-rate in crystals (metals, semiconductors).

In crystals, band structure calculations lead to an effective mass for the charge carriers, which can be negative. Inspired by the Hall Effect, Newton's law is used to attach the negative sign onto the charge.

13-3 In quantum mechanics, and in particular quantum chemistry, the electronic density is a measure of the probability of an electron occupying an infinitesimal element of space surrounding any given point. It is a scalar quantity depending upon three spatial variables and is typically denoted as either ρ(r) or n(r). The density is determined, through definition; by the normalized N-electron wave function which itself depends upon (4N) variables (3N spatial and N spin coordinates). Conversely, the density determines the wave function modulo a phase factor, providing the formal foundation of density functional theory.

13-4 An integrated circuit: or monolithic integrated circuit (also referred to as IC, chip, or microchip) is an electronic circuit manufactured by lithography, or the patterned diffusion of trace elements into the surface of a thin substrate of semiconductor material. Additional materials are deposited and patterned to form interconnections between semiconductor devices.

13-5 Electrical mobility: is the ability of charged particles (such as electrons or protons) to move through a medium in response to an electric field that is pulling them. The separation of ions according to their mobility in gas phase is called Ion mobility spectrometry, in liquid phase it is called electrophoresis.

13-6 Semiconductor materials: are nominally small band gap insulators. The defining property of a semiconductor material is that it can be doped with impurities that alter its electronic properties in a controllable way.

Because of their application in devices like transistors (and therefore computers) and lasers, the search for new semiconductor materials and the improvement of existing materials is an important field of study in materials science.

Most commonly used semiconductor materials are crystalline inorganic solids. These materials are classified according to the periodic table groups of their constituent atoms.

14- An organic semiconductor is an organic material with semiconductor properties. Single molecules, short chain (oligomers) and organic polimers can be semiconductive. Semiconducting small molecules (aromatic hydrocarbins) include the polycyclic aromatic compounds pentacene, anthracene, and rubrene. Polymeric organic semiconductors include poly(3-hexylthiophene), poly(p-phenylene vinylene), as well as polyacetylene and its derivatives. There are two major overlapping classes of organic semiconductors. These are organic charge-transfer complexes and various linear-backbone conductive polymers derived from polyacetylene. Linear backbone organic semiconductors include polyacetylene itself and its derivatives polypyrrole, and polyaniline. At least locally, charge-transfer complexes often exhibit similar conduction mechanisms to inorganic semiconductors.

15- A charge-transfer complex (CT complex) or electron-donor-acceptor complex is an association of two or more molecules, or of different parts of one very large molecule, in which a fraction of electronic charge is transferred between the molecular entities. The resulting electrostatic attraction provides a stabilizing force for the molecular complex. The source molecule from which the charge is transferred is called the electron donor and the receiving species is called the electron acceptor.

The nature of the attraction in a charge-transfer complex is not a stable chemical bond, and is thus much weaker than covalent forces. The attraction is created by an electronic transition into an excited electronic state, and is best characterized as a weak electron resonance. The excitation energy of this resonance occurs very frequently in the visible region of the electro-magnetic spectrum, which produces the usually intense color characteristic for these complexes. These optical absorption bands are often referred as charge-transfer bands (CT bands). Optical spectroscopy is a powerful technique to characterize charge-transfer bands.

Conclusion from definitions:

The line vector function is the shortest function with respect to time. The uncertainty principle missed to use this function to deal with time frequency, in contradiction the principle was based on Fourier transform which makes the time frequency more complicated and less fast, means a loss of time during the process. The consequences are to limit the development of applications in many domains of technologies such as instruments of measurement used in quantum mechanics, and in the computer based applications.

I already introduced three materials (TiCuO, DyCuO, and SiCuO), these materials are compounds of copper and oxygen called cuprates, they are a new family of high temperature superconductor, and can resolve the problem of room temperature superconductor and also they could be the solution to resolve the problem cited above. Once a chip and a transistor are built using these materials; efficiency in time frequency will be corrected at 100%. This is a huge gain of time by achieving C in E =MC2. The problem of the observer of particles and wave like particles will be resolved; means it will be possible to see a particle as a particle and as a wave in the same time. Also most of the persisting problems within the OSI model will be resolved by adding an 8^th layer which is chips and transistors based on (TiCuO, DyCuO and SiCuO).

The suggested materials are organic metals designed in molecule shape, and they are superconductors formed illegally to the human known physics laws. 

TiCuO, DyCuO and SiCuO reflecting light on BECs surface due the high electron density.

TiCuO, DyCuO and SiCuO reflecting light on BECs surface due the high electron density.

TiCuO, DyCuO and SiCuO reflecting light on BECs surface due the high electron density.

Note: Definitions are from Wikipedia